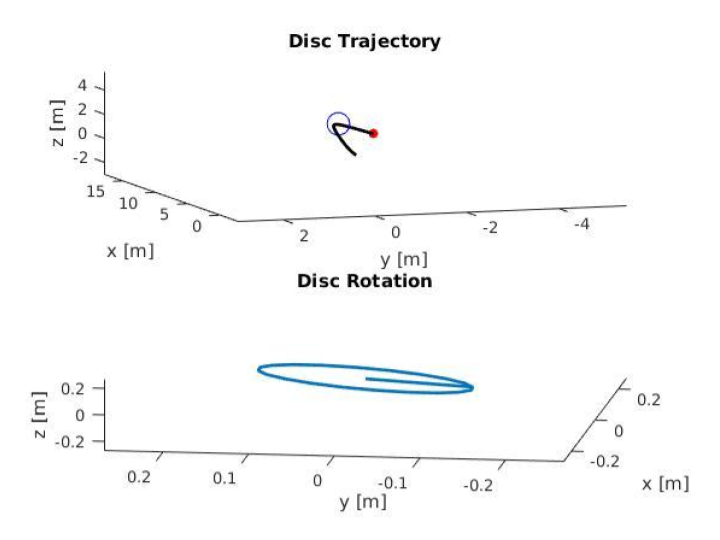
Frisbee Simulator
Overview: This Frisbee Simulator accurately models the flight of a frisbee. By deriving the translational and rotational dynamics of a frisbee flying through the air, I developed equations of motion that were then mapped to a state space model that was integrated forward in time using MATLAB to solve for the pose of the disc as a function of time. I also used optimization techniques to solve for an initial set of throwing parameters to aim a frisbee throw to a target somewhere in 3D space. More details regarding my project, including videos, can be found below. If you are interested in learning about the math and physics behind it all, check out the white paper linked below.
White Paper: https://drive.google.com/open?id=0B81gni53B9VOMHkzZ09VcUNiMm8
Source Code: https://drive.google.com/open?id=0B81gni53B9VOa0ZMRVQ1QVZqZlE
Basic Flight Examples:
Below are a few examples of various flight paths of a frisbee given a range of initial conditions. Here the initial conditions represent the way the frisbee is release (rotational velocity, release angles, height off of ground). The simulator can also model various types of throws including the classic forehand (flick) and backhand throws. Those experienced with the game of Ultimate will hopefully notice how the simulator accurately models realistic phenomena such as the air bounce, inside-out and outside-in throws, and disc tailing off at the end of their flight.
Basic Flight
Example of Flick Tailing Right
Example of Backhand Tailing Left
Even cooler still, is the simulators ability to model how a frisbee's tendency to tail is based on the amount of spin (or rotational inertia) it has during flight. Here we can see how a disc released with less rotational velocity will tail off much more significantly at the end of its flight.
Large Tailing Due To Low Spin
Aiming a Throw Using Optimization:
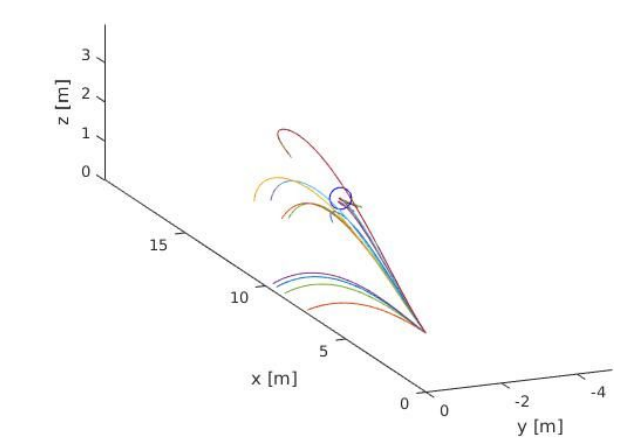
The simulator can also "learn" to throw a frisbee to a desired location (or through a hoop) using optimization techniques. To do so, the simulator must take in a desired position in space the user wants the frisbee to fly to. Then it will iteratively attempt to throw to the specified target, measure the error, and tweak the initial conditions of the throw to decrease the error until the flight succeeds.
Below is a figure of the various attempts that the simulator makes before finally completing a throw that makes it through the hoop.
